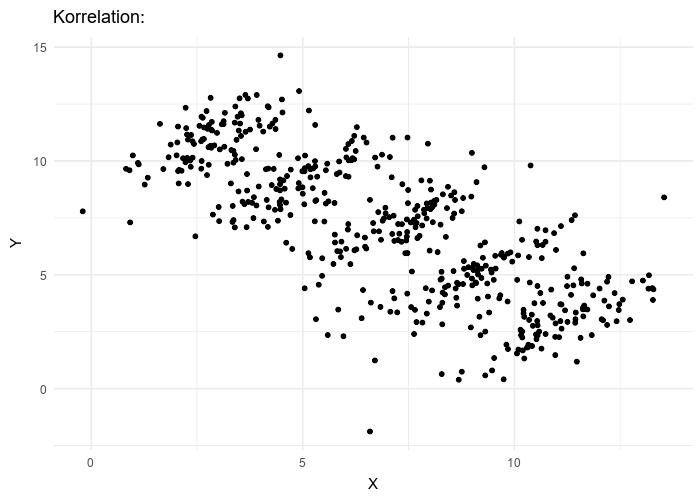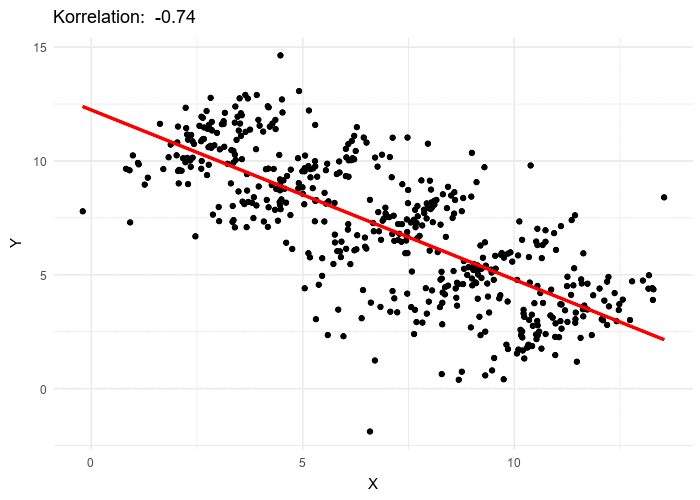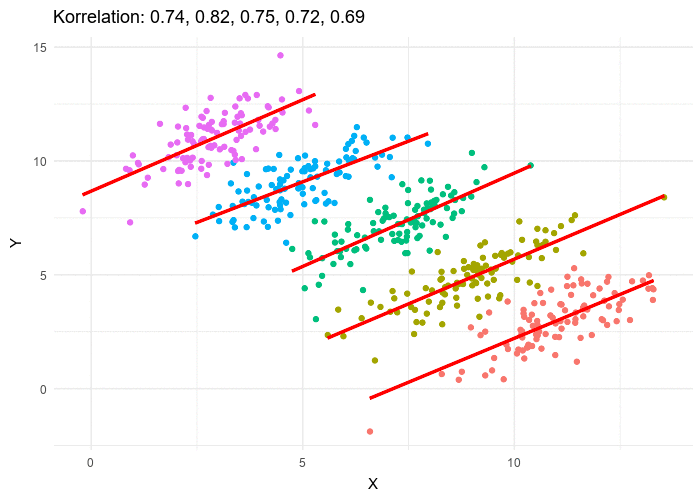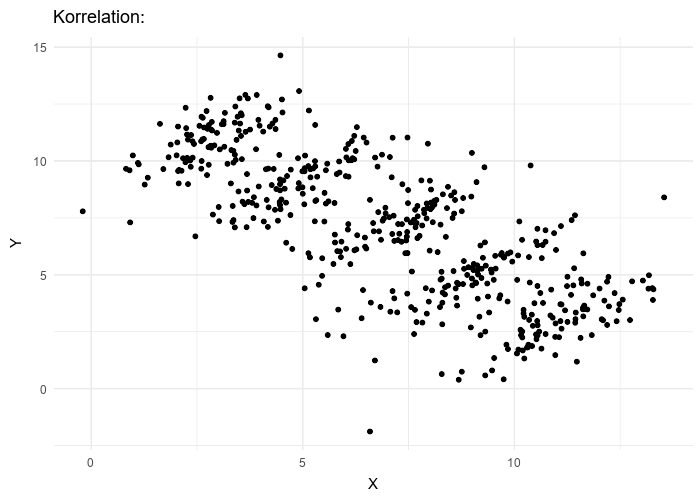
辛普森悖论（simpson’s paradox），是概率和统计中的一种现象，其中趋势出现在几组数据中，但当这些组被合并后趋势消失或反转。这个结果在社会科学和医学科学统计中经常遇到，当频率数据被不恰当地给出因果解释时尤其成问题。当干扰变量和因果关系在统计建模中得到适当处理时，这个悖论就可以得到解决。 辛普森悖论已被用来说明统计误用可能产生的误导性结果。

关于辛普森悖论的论述推荐知乎上两篇高赞回复

1. 关于辛普森悖论的深度解析
2. 真实的谎言——辛普森悖论面面观

而本文的主题是当博主在工作中遇到辛普森悖论时如何去量化根因(打脸业务我的数据没有出问题)

一、背景

在ToC产品领域，用户粘性体现了用户反复与产品交互的倾向，粘性越高的产品对用户而言越重要，更能吸引用户定期使用并提升忠诚度。粘性的计算通常与日活跃用户数（DAU）和月活跃用户数（MAU）密切相关。博主所在的国内知名软件数据团队，曾遇到这样的业务反馈：首页的粘性指标呈现持续增长态势，然而深入查看各子页面的粘性却无一例外地出现下降。这不禁引发疑问，数据是否出现了问题？

在自行检查计算逻辑无误后，又从底层数据表对指标进行了复核，进一步确认数据并无异常。通过拉长时间范围进行观察，博主发现粘性指标的几个关键拐点均与实验调整（用户组发生变化）相吻合。基于此，推测可能是用户结构的变动、用户更多地涌入高粘性页面导致了这一看似矛盾的现象。显然，业务团队陷入了辛普森悖论的误区。那么，如何向业务团队清晰地阐释并非数据问题，而是用户结构变化引发的现象，并给出科学合理的根本原因解释呢？这就需要借助专业的数据分析方法和工具来进行详细解读。

二、量化根因

使用贡献度分解法(LMDI 分解法)针对辛普森悖论进行分析，思想是将整体指标变化拆解为群体效应（粘性变化）、结构效应（权重变化）和交互效应（粘性和权重之间的协同作用）。

1. 群体效应
   1. 定义：反映了每个部分自身粘性变化对整体粘性的影响。它衡量了如果用户结构保持不变，仅由于各部分自身粘性变化所带来的整体粘性变化
   2. 解释：结合背景就是子页面自身的粘性变化情况
2. 结构效应
   1. 定义：用户群体权重变化对整体粘性的影响。具体来说，它衡量了如果每个部分的粘性保持不变，仅由于各部分用户占比发生变化所带来的整体粘性变化。
   2. 解释：结合背景就是隐藏幕后的人群结构的变化
3. 交互效应：
   1. 定义：反映了粘性变化和权重变化之间的交互作用。它衡量粘性变化和权重变化同时发生时的联合影响
   2. 解释：可以理解为一种加权，但交互效应通常较小。结合业务可以反应一些底层逻辑，例如：某个页面交互效应为负，表明该页面用户占比增加（结构效应为正）但粘性降低（群体效应为负），显然该页面需要被重点关注

结合背景用LMDI去解释粘性变化问题就是：虽然群体效应为负（子页面粘性在降低）但有足够多的正向的结构效应（实验调整各用户组的比例）抵消了负向群体效应让整体效应呈现正向

下面是三种效应的计算公式：
$$
\begin{align*}
\Delta S_{\text{struct}} &= \sum_i S_{0_i} \times (W_{1_i} - W_{0_i})
\end{align*}
$$
$$
\begin{align*}
\Delta S_{\text{group}} &= \sum_i W_{0_i} \times (S_{1_i} - S_{0_i})
\end{align*}
$$
$$
\begin{align*}
\Delta S_{\text{interact}} &= \sum_i (S_{1_i} - S_{0_i}) \times (W_{1_i} - W_{0_i})
\end{align*}
$$

三、SQL实现

假设首页记作 main，下挂五个子页面分别是：p1、p2、p3、p4、p5。在进行LMDI分解前需要准备好每个页面粘性的原子指标（dau 和 mau）并选择”数据异常”时间(期初)和一个对照时间(期末)，二者大小、前后没有要求

@basic_data:
select dt, page_name, dau, mau from ads_page_active_di where dt in ('期初时间', '期末时间');

step-1: 计算权重 w

@base_data: 
select 
  dt,
  page_name,
  dau / mau as stickiness,
  mau / first_value(mau) over(partition by dt order by if(page_name = 'main', 1, 0) desc) as weight
from basic_data

step-2: 计算指标变化率

@metrics_change:
select 
    t1.page_name,
    t1.stickiness as stickiness_t1,
    t2.stickiness as stickiness_t2,
    t2.stickiness - t1.stickiness as stickiness_delta,
    t1.weight as weight_t1,
    t2.weight as weight_t2,
    t2.weight - t1.weight as weight_delta
from (
    select * from base_data where dt = '期初时间'
) t1 join (
    select * from base_data where dt = '期末时间'
) t2 on t1.page_name = t2.page_name

step-3: 计算每个页面三种效应

@simpson_decomposition:
select 
    page_name,
    stickiness_t1,
    stickiness_t2,
    stickiness_delta,
    weight_t1,
    weight_t2,
    weight_delta,
    -- 群体效应 = 期初权重 * 粘性变化
    weight_t1 * stickiness_delta as group_effect,
    -- 结构效应 = 期初粘性 * 权重变化
    stickiness_t1 * weight_delta as struct_effect,
    -- 交互效应 = 粘性变化 * 权重变化
    stickiness_delta * weight_delta as interaction_effect,
    -- 总效益 = 群体效应 + 结构效应 + 交互效应
    (weight_t1 * stickiness_delta) + (stickiness_t1 * weight_delta) + (stickiness_delta * weight_delta) as total_effect
from metrics_change

step-4: 计算整体效应

select 
    '所有子页面辛普森悖论分解' as type,
    'all' as page_name,
    sum(group_effect) as group_effect,
    sum(struct_effect) as struct_effect,
    sum(interaction_effect) as interaction_effect,
    sum(total_effect) as total_effect
from simpson_decomposition where page_name <> 'main'
union all
select 
    '子页面辛普森悖论分解' as type,
    page_name,
    group_effect,
    struct_effect,
    interaction_effect,
    total_effect
from simpson_decomposition where page_name <> 'main'

可以发现每个页面的的群体效应都是负向，表明自身粘性均在降低，但结构效应除 p2 外均成正向，最终整体效应为0.00019

需注意，以上LMDI分解结果数据均为虚构，仅用于解释说明。在实际进行整体拆解时，要确保拆解全面且各部分相互独立，避免出现交叉重叠，以保证分析的准确性和可靠性。

四、专业报告解读

引入 AI 生成更加专业的报告解读并将分析结果作为上下文。可以参考的prompt如下：

上下文中给出的是使用辛普森悖论分解（LMDI 分解法）得出的五个子页面以及整体的群体效应、结构效应、交互效应、整体效应；使用 html 编写这份报告，这份曝光的目的是向业务解释为什么子页面粘性降低但整体粘性却在增长的辛普森悖论

最终效果如下（点击预览文件）